푸리에 변환 완벽 가이드: 주파수 분석의 모든 것

푸리에 작성
작성일 2024.12.22 20:22

286 조회
목록

이 게시물에는 제가 경제적 이익을 얻을 수 있는 제휴 링크가 포함되어 있습니다.

푸리에 변환에 대한 정보를 찾고 계신가요? 신호 처리, 이미지 분석, 음향 공학 등 다양한 분야에서 필수적인 개념인 푸리에 변환에 대해 쉽고 명확하게 설명드립니다. 본 가이드에서는 푸리에 변환의 원리, 종류, 활용 예시, 그리고 최신 트렌드까지 알차게 담았습니다. 지금 바로 푸리에 변환의 세계를 탐험해보세요!

푸리에 중요 정보 요약

푸리에 변환이란 무엇일까요? 시간 영역 신호를 주파수 영역 신호로 변환하는 수학적 도구입니다.
푸리에 변환의 주요 활용 분야는 무엇일까요? 신호 처리, 이미지 처리, 음향 공학, 의료 영상 등 다양한 분야에서 활용됩니다.
푸리에 변환의 종류에는 어떤 것들이 있을까요? 푸리에 급수, 푸리에 변환, 이산 푸리에 변환 (DFT), 고속 푸리에 변환 (FFT) 등이 있습니다.
푸리에 변환을 효과적으로 활용하려면 무엇을 알아야 할까요? 기본적인 수학적 지식과 신호 처리 개념에 대한 이해가 필요합니다.
최근 푸리에 변환 분야의 트렌드는 무엇일까요? 딥러닝과의 결합, 실시간 신호 처리 기술 발전 등이 주요 트렌드입니다.

용어	설명
푸리에 변환	시간 영역 신호를 주파수 영역 신호로 변환하는 수학적 변환
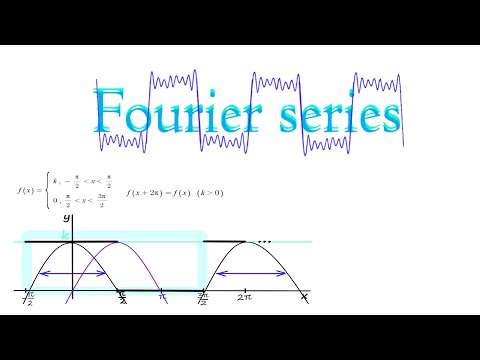
푸리에 급수	주기적인 신호를 사인파와 코사인파의 합으로 표현하는 방법
이산 푸리에 변환 (DFT)	디지털 신호를 주파수 영역으로 변환하는 방법
고속 푸리에 변환 (FFT)	DFT의 계산 속도를 획기적으로 향상시킨 알고리즘
주파수 스펙트럼	푸리에 변환 결과로 얻어지는 신호의 주파수 성분 분포

이미지 클릭시 할인 정보 상품 링크로 연결됩니다.

푸리에 변환이란 무엇일까요? 왜 중요한가요?

푸리에 변환은 복잡한 신호를 구성하는 기본적인 주파수 성분들을 분석하는 강력한 도구입니다. 마치 오케스트라의 복잡한 음악을 개별 악기의 소리로 분해하는 것과 같습니다. 시간 영역에서 관찰하기 어려운 신호의 특징을 주파수 영역에서 명확하게 파악할 수 있게 해줍니다. 이를 통해 신호의 특징을 추출하고, 노이즈를 제거하고, 신호를 압축하는 등 다양한 작업을 수행할 수 있습니다. 예를 들어, 음악 파일의 압축, 이미지의 잡음 제거, 의료 영상 분석 등 다양한 분야에서 핵심적인 역할을 합니다.

푸리에 변환의 다양한 종류와 그 차이점은 무엇일까요?

푸리에 변환에는 여러 가지 종류가 있으며, 각각의 특징과 활용 분야가 다릅니다.

변환 종류	설명	활용 분야
푸리에 급수	주기적인 신호를 사인 및 코사인 함수의 무한 합으로 표현합니다.	주기 신호 분석, 신호 합성
푸리에 변환	비주기적인 신호를 주파수 성분으로 분해합니다.	신호 분석, 시스템 해석
이산 푸리에 변환 (DFT)	디지털 신호에 적용되는 푸리에 변환으로, 유한 개의 샘플을 사용합니다.	디지털 신호 처리, 이미지 처리
고속 푸리에 변환 (FFT)	DFT의 계산 속도를 획기적으로 향상시킨 알고리즘입니다.	실시간 신호 처리, 큰 데이터셋 분석, 이미지/음성 인식 등

팁: FFT 알고리즘은 DFT보다 훨씬 빠르게 계산되므로, 실시간 신호 처리나 대용량 데이터 처리에 필수적입니다.

푸리에 변환을 어떻게 활용할 수 있을까요? 실제 예시와 함께 설명해주세요.

푸리에 변환은 다양한 분야에서 활용됩니다. 몇 가지 대표적인 예시를 살펴봅시다.

음악 및 오디오 처리: 음악 파일의 압축 (MP3), 음성 인식, 노이즈 제거 등에 사용됩니다. 각 주파수 성분의 크기를 분석하여 중요한 정보만 저장하거나 노이즈 주파수를 제거하는 방식으로 활용됩니다.
이미지 처리: 이미지의 잡음 제거, 이미지 압축, 특징 추출 등에 사용됩니다. 이미지를 주파수 영역으로 변환하여 고주파 성분(잡음)을 제거하거나 저주파 성분만을 이용해 이미지를 압축할 수 있습니다.
의료 영상: MRI, CT 등 의료 영상의 분석에 사용됩니다. 영상의 주파수 성분을 분석하여 질병 진단에 필요한 정보를 추출합니다.
통신: 신호 전송 및 수신 과정에서 신호의 변조 및 복조, 채널 등화 등에 사용됩니다.

이미지 클릭시 할인 정보 상품 링크로 연결됩니다.

푸리에 변환과 최신 기술 트렌드: 딥러닝과의 만남

최근에는 푸리에 변환이 딥러닝과 결합하여 더욱 강력한 성능을 발휘하고 있습니다. 딥러닝 모델은 푸리에 변환을 통해 얻어진 주파수 정보를 입력으로 사용하여 이미지 분류, 음성 인식 등의 성능을 향상시키고 있습니다. 또한, 실시간 신호 처리 기술의 발전으로 푸리에 변환을 활용한 응용 프로그램의 개발이 가속화되고 있습니다. 이는 사물 인터넷(IoT), 자율주행 자동차 등 다양한 분야에서 혁신을 가져올 것으로 예상됩니다.

이미지 클릭시 할인 정보 상품 링크로 연결됩니다.

결론: 푸리에 변환, 미래를 향한 핵심 기술

본 가이드를 통해 푸리에 변환의 개념, 종류, 활용, 그리고 최신 트렌드를 이해하셨기를 바랍니다. 푸리에 변환은 다양한 분야에서 필수적인 기술이며, 앞으로도 그 중요성이 더욱 커질 것입니다. 이 가이드가 푸리에 변환을 더 잘 이해하고 활용하는 데 도움이 되기를 바랍니다. 더 깊이 있는 학습을 원하신다면 관련 서적이나 온라인 강의를 참고하시기 바랍니다.

상품상세보기 : 푸리에 상품 비교, 할인정보 바로가기

질문과 답변

푸리에 변환이란 무엇인가요? 2024-12-23

푸리에 변환은 시간 영역의 신호를 주파수 영역의 신호로 변환하는 수학적 도구입니다. 복잡한 파형을 다양한 주파수의 사인파와 코사인파의 합으로 분해하여 각 주파수 성분의 크기와 위상을 분석할 수 있게 해줍니다. 쉽게 말해, 어떤 소리나 신호가 어떤 주파수의 성분으로 이루어져 있는지 알려주는 것이라고 생각하면 됩니다.

푸리에 변환은 어디에 사용되나요? 2024-12-23

푸리에 변환은 다양한 분야에서 활용됩니다. 음성 인식, 이미지 처리, 의료 영상 분석, 신호 처리, 통계학 등에서 데이터 분석 및 처리에 필수적인 도구로 사용됩니다. 예를 들어, MP3 파일 압축이나 MRI 영상 생성 등에 활용됩니다.

푸리에 변환의 종류에는 무엇이 있나요? 2024-12-23

대표적으로 푸리에 급수, 푸리에 변환, 이산 푸리에 변환(DFT), 고속 푸리에 변환(FFT) 등이 있습니다. 급수는 주기적인 신호에, 변환은 비주기적인 신호에 사용되며, DFT와 FFT는 디지털 신호 처리에 적합하도록 변형된 형태입니다. FFT는 DFT보다 계산 속도가 훨씬 빠르다는 장점이 있습니다.

푸리에 변환을 이해하기 위해 어떤 배경지식이 필요한가요? 2024-12-23

미적분학과 복소수에 대한 기본적인 이해가 필요합니다. 특히 삼각함수와 지수함수에 대한 지식이 중요하며, 선형대수학의 기본적인 개념을 알고 있다면 더욱 효과적으로 이해할 수 있습니다. 하지만 수학적 배경이 부족하더라도 개념적인 이해를 위해 쉽게 설명된 자료들을 참고할 수 있습니다.

푸리에 변환을 직접 구현하려면 어떻게 해야 하나요? 2024-12-23

프로그래밍 언어(예: 파이썬, MATLAB)를 이용하여 푸리에 변환을 직접 구현할 수 있습니다. 각 언어는 푸리에 변환을 위한 라이브러리를 제공하므로, 이를 이용하여 손쉽게 구현이 가능합니다. 또한, FFT 알고리즘을 사용하면 계산 효율을 높일 수 있습니다. 온라인 강의나 튜토리얼을 통해 구현 방법을 학습할 수 있습니다.

네이버백과 검색 네이버사전 검색 위키백과 검색

푸리에 관련 동영상